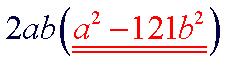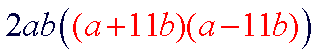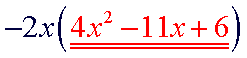|
Factor:
|
|
||
| This expression has two terms. There is a common factor of 2ab. Begin by factoring out the common factor. |
|
||
| The remaining factor is a binomial that is the difference of two squares. This factor must be factored using the difference of two squares technique. |
|
||
| Each of the new factors must in turn be checked for further factoring. In this case, no further factoring can be done. Our final answer is 2ab(a+11b)(a-11b) |
|
||