Factor:
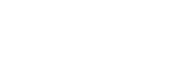
![]()
![]()
![]()
![]()
|
Factor:
|
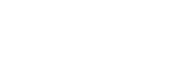 |
||
| This expression has two terms. The variable x is a common factor in both terms. |
|
||
| x can be divided out of each term |
|
||
| The common factor x is "undistributed" and placed to the left of a set of parentheses. The remaining factors are placed inside the parentheses. |
|
||
|
Factor:
|
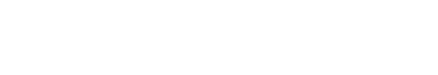
|
||
| This expression has three terms. Each term has a common factor of 3 x2 y. |
|
HINT:
|
|
|
3
x2 y
can be divided out of
each term.
But what happens to the last term? All the factors are divided out, therefore 1 is left. |
|
||
|
Check the remaining factor to be sure there is no common factor. If there is, then you did not extract the GREATEST common factor to begin with. |
|
|
|
|
Factor:
|
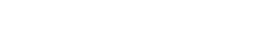
|
||
| This expression has three terms. There is no common factor shared by ALL three terms. There is no GCF. Furthermore, the expression cannot be factored. |
|
NOTE: Always check for a common factor. If you cannot find one, look for other factoring patterns. If no other factoring patterns apply then you can conclude that the expression cannot be factored. Such and expression is called PRIME. |
|
|
|
|||