 |
 |
||
|
|
|||
|
|
|||
|
|
|
||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
|
Product with same base |
|
When multiplying like bases, keep the base the same and add the exponents. |
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| Power to a Power |
|
When raising a base with a power to another power, keep the base the same and multiply the exponents. |
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| quotient with same base | 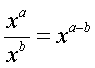 |
When dividing like bases, keep the base the same and subtract the denominator exponent from the numerator exponent. |
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| Product to a Power | When raising a product to a power, distribute the power to each factor. |
|
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| quotient to a Power | 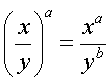 |
When raising a fraction to a power, distribute the power to each factor in the numerator and denominator of the fraction. |
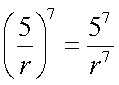
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| zero power | Anything raised to the zero power is one. |
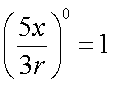
|
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| negative power | 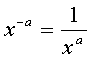 |
Negative
exponents signify division. In particular, find the reciprocal of the
base.
When a base is raised to a negative power, reciprocate (find the reciprocal of) the base, keep the exponent with the original base, and drop the negative. |
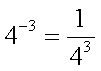
|
|
|
|||
|
|
|||
|
Description |
in Symbolic form |
The
Rule in Words |
Example |
| quotient with negative power | 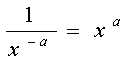 |
Negative
exponents signify division. In particular, find the reciprocal of the
base.
When a denominator is raised to a negative power, move the factor to the numerator, keep the exponent but drop the negative. |
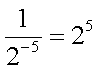
|
|
|
|||
|
|
|||