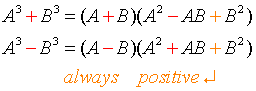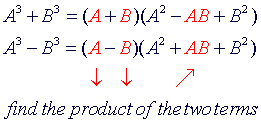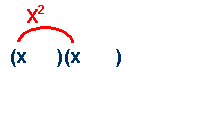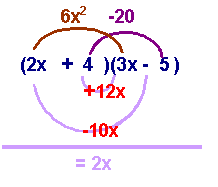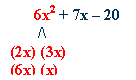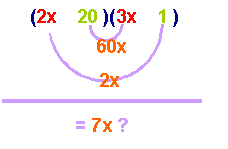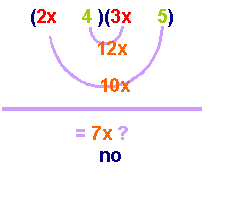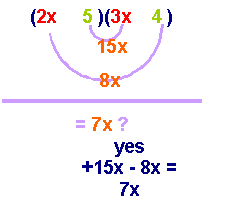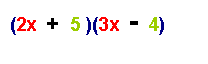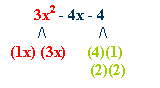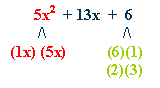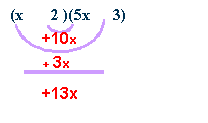|
FACTORING
TECHNIQUES: Binomials |
|
types |
A binomial
is an expression containing two terms. Aside from factoring out the
greatest common factor, there are three types of special binomials that
can be factored using special techniques. These special binomials are:
|
|
|
|
-
The
Difference of Squares:
|
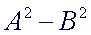
|
- the
first term is a perfect square: AxA
- the
second term is a perfect square: BxB
- the
two terms are being subtracted
|
|
|
|
|
|
-
The
Sum of Cubes:
|
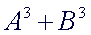
|
- the
first term is a perfect cube: AxAxA
- the
second term is a perfect cube:
BxBxB
- the
two terms are being added.
|
|
|
-
The
Difference of Cubes:
|
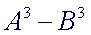
|
- the
first term is a perfect cube: AxAxA
- the
second term is a perfect cube:
BxBxB
- the
two terms are being subtracted
|
|
|
|
To find out more about
how to factor these special binomials, click on one of the links below: |
|
|
|
|
|
Note:
The sum of squares is not factorable unless there is a common factor. |
|
|
|
The
sum of squares: |
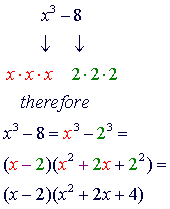
|
cannot
be factored with integer coefficients. |
|
|
Many
beginners believe that the sum of squares is factorable as follows:
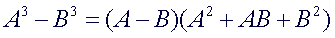
|
This
misconception can be easily dispelled by checking. That is, multiply out
the factored form:

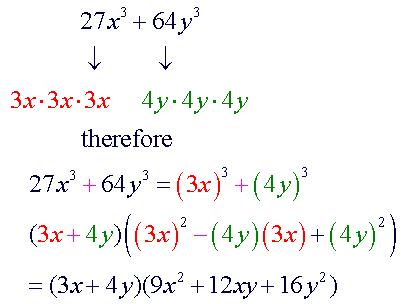
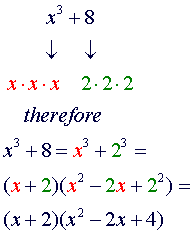 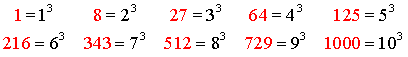
|
 |
|
The
sum of squares can be factored with real
numbers only if there
is a common factor. Here is an example: |

|
|
|
|
|
|
|
|
FACTORING
TECHNIQUES: Difference of Squares |
|
|
 |
|
Difference
of squares |
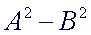 |
Factoring the difference of squares
|
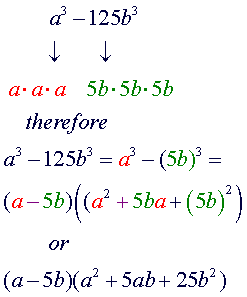
 |
|
|
EXAMPLE
1 |
|
EXAMPLE
2 |
|
|
|

|
|
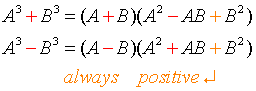
|
|
|
|
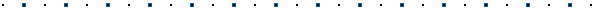
To
factor the difference of two squares
it is useful to know the integers
that are perfect squares. Here are the first 20:
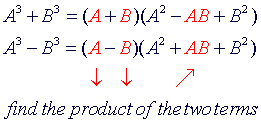
|
|
|
|
|
|
|
|
|
FACTORING
TECHNIQUES: Sum of Cubes |
|
|
 |
|
Sum
of cubes |
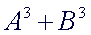 |
Factoring the sum of
cubes |
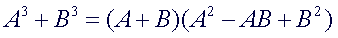

|
|
|
EXAMPLE
1 |
|
EXAMPLE
2 |
|
|
|
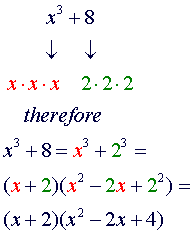
|
|
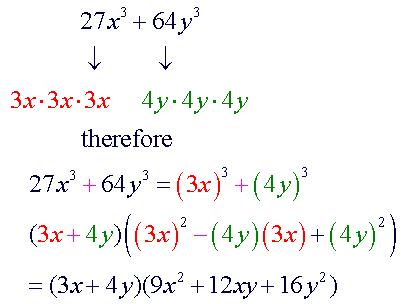
|
|
|
|
The
factorization of x3 + y3 has a first factor of x +
y, where x and y are the roots
or the numbers that must be cubed to obtain each term. The second factor
has three
terms with the following pattern:
Looking
at the first factor, x + y
-
the
first term of the second factors is the square of the first term of
the first factor.
-
the
second term of the second factor is the negative
product of the
two terms of the first factor
-
the
third term of the second factor is the square of the second term of
the first factor.
To
factor the sum of two cubes it is useful to know the integers
that are perfect cubes. Here are the first 10:
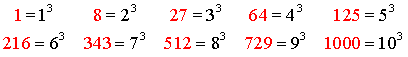
|
|
|
|
|
|
|
|
FACTORING
TECHNIQUES: Difference of Cubes |
|
|
 |
|
difference
of cubes |
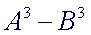 |
Factoring the difference
of cubes |
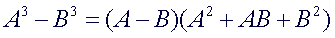

|
|
|
EXAMPLE
1 |
|
EXAMPLE
2 |
|
|
|
|
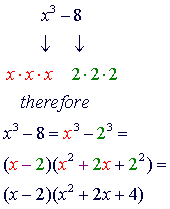
|
|
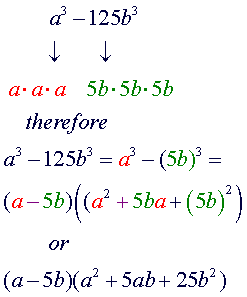
|
|
|
|
|
|
The
factorization of the difference of cubes is similar to the factorization
of the sum of cubes. The only difference between the two are the signs.
Here are some observations to keep in mind:
-
The
first factor in each will always have the same sign as the original
problem. The second term of the second factor will always have the
opposite sign. The last term of the second factor will always be
positive.

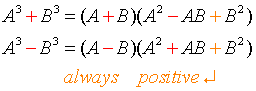
-
The
middle term of the second factor is the product of the terms of the
first factor.
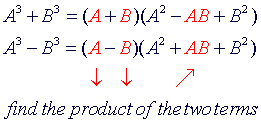
|
|
 |
|
|
|
|
|
|
|
|
|
|
FACTORING
TECHNIQUES: Trinomials |
|
Trinomials
|
The
product of two binomials is usually a trinomial. A trinomial is an
expression containing
three terms. For example:
-
(x
+ 4)(x - 5) = x2 - 5x + 4x - 20 = x2
- x - 20
-
(3x
+ 5)(2x - 7) = 6x2 -21x + 10x - 35 = 6x2
- 11x - 35
There
are two types of products.
The first example is a trinomial with a leading coefficient of 1:
x2
- x - 20 = 1x2
- x - 20
The
second example is a trinomial with a leading coefficient not equal to one:
6x2
- 11x - 35 = 6x2
- 11x - 35
The
technique used for factoring trinomials will depend on whether or not the
leading coefficient is a one.
Factoring
Trinomials with a leading coefficient of one
It
is important to understand where these trinomials come from. The patterns
that produce them will be the patterns that we use to reverse the process.
Notice the following pattern when multiplying two binomials:
|
- The
first two terms are identical and multiply to make x2
- The
second two terms multiply to make the last term of the trinomial. They
are factors of the last term.
- The
middle term is the sum of the factors of the last term.
|
(x
+ 4)(x
- 5)
x2
- 5x + 4x - 20
x2
- x - 20 |
|
|
These
observations can be used to go backwards. To factor a trinomial with
leading coefficient of one, we need to look at the two binomials that
generated this product. Consider, for example, the following:
Factor:
x2 + 5x + 6
step
1:
Open up two sets of parentheses. The first term in each must multiply
together to get x2.
This must be x and x.
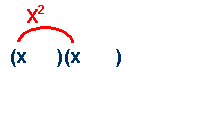
step
2:
Determine
the factors of the last term. It is helpful to make a list to refer to.
Include the appropriate sign. If a term is positive, the factors will
have the same sign: (+)(+) or (-)(-). If the term is negative, the
factors will have opposite signs. (+)(-). In our example, we need like
signs.
x2 + 5x +
6
/ \
(+3)(+2)
or (-3)(-2)
(+6)(+1)
0r (-3)(-2)

step
3:
Choose
the factors whose sum will produce the coefficient of the middle term.
If the last term is positive,
the middle number will be the result of an addition.
If the last term is
negative, the
middle number will be the result of a
subtraction.

In
this case +3 and +2 will multiply to make +6 and combine to make +5.
Here are a few more example to review. Pay close attention to the signs.
|
|
EXAMPLE
1 |
EXAMPLE
2 |
EXAMPLE
3 |
EXAMPLE
4 |
|
a2
+2a - 15 |
y2
- 7y + 12 |
x2
- 4x - 21 |
x2
+ xy - 6y2 |
|
a2 +2a - 15
/\
/\
a
a
(+3)(-5)
(-3)(+5)
(-1)(+15)
(+1)(-15) |
y2 - 7y + 12
/\
/\
y
y
(-1)(-12)
(-1)(-12)
(+1)(+12)
(-3)(-4)
(-6)(-2)
(+6)(+2)
|
x2 - 4x - 21
/\
/\
x
x
(-21)(+1)
(+21)(-1)
(+7)(-3)
(-7)(+3) |
x2
+ xy - 6y2
/\
/\
x
x
(-6y)(+y)
(+6y)(-y)
(+3y)(-2y)
(-3y)(+2y) |
|
-3
and +5 yield +2 |
-3
and -4 yield -7 |
-7
and + 3 yield -3 |
+3y
and -2y yield -6y2 |
|
(a
- 3)(a + 5) |
(y
- 4)(y - 3) |
(x
- 7)(x + 3) |
(x + 3y)( x -
2y) |
Factoring
Trinomials when the leading coefficient
is not one
We
will begin by looking a the pattern of multiplication of two binomials. Notice
the following: |
- The
first two terms multiply to make 6x2
- The
second two terms multiply to make the last term of the trinomial. They
are factors of the last term.
- The
middle term, is much more complicated. It is the sum of the outer and
inner products of the binomial factors. This will be the key to
finding the correct factors.
|
(2x
+ 4)(3x
- 5)
6x2
- 5(2x)
+ 4(3x)
- 20
6x2
- 10x + 12x - 20
6x2
+ 2x - 20
|
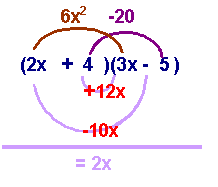 |
|
Working
backwards to factor can be a challenge. Always check your answers.
Patience and practice will go a long way. Consider the following:
Factor:
6x2 + 7x - 20
step
1:
Open up two sets of parentheses. The first term in each must multiply
together to get 6x2.
List all the options for the first terms. Do not place them in the parentheses.
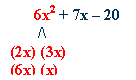

step
2:
Skip
to the last term. List all the factor options for the last term.
Do not place them in the parentheses. Ignore the signs of your terms for
now. This narrows our choices down for finding the middle term.
 
step
3:
Begin
a trial and error process. Choose one pair of factors from the first
list and one pair of factors from the second list.
For
example we might choose (2x)(3x)
and (20)(1).
Multiply
one factor from list one with one factor of list two, then multiply the
"partners". Check to see if the products will combine to make
the middle term.
For
example: (2x)(1)=
2x and (3x)(20)
= 60x but 2x and
60x will not make 7x by addition or subtraction.
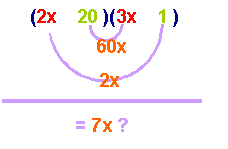
Note
that (2x)(20)=
40x and (3x)(1)
= 3x yields
another option, yet one that again does not work. Continue pairing off
factors until you find two products that will produce the middle
term.
Helpful
HintS:
Try the smaller numbers first. Usually the numbers that differ by
a smaller quantity are more likely to be the factors.
For
example, here we might want to try (2x)(3x)
in combination
with (5)(4).
Also,
try to make a product that is close to the middle number. Here, for
example, we might choose (2x)(5x)
or (3x)(5x)
(2x)(5)
= 10
(3x)(4) =
12
__________________
(2x)(4)
= 8
(3x)(5) =
15
These
are the two possibilities:
OR
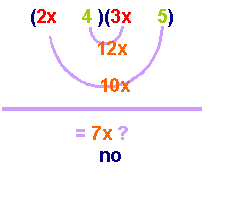
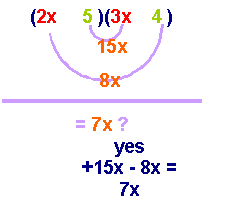
step
4:
Once
you have found the correct combination, place the appropriate sign with
the second term according to the desired product. We need the middle
term to be positive, so the larger product [15x] must be positive. Since
we need 15x to be positive, make the 5 positive. We need the 8x to be
negative so the 4 must be negative.
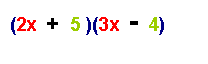
step
5:
Check
by multiplying the two binomials.
(2x
+ 5)(3x - 4) = 6x2 - 8x + 15x - 20 = 6x2 +
7x - 20 þ
Here
are two more examples to review: |
|
Example
1 |
Example
2 |
|
Factor:
3x2 - 4x - 4
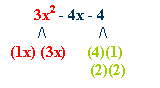
try
(x)(3x)
with (2)(2)
(x)(2)
and (3x)(2)
2x and 6x will yield 4x

(x
- 2)(3x + 2)
|
Factor:
5x2 + 13x + 6
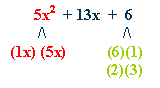
try
(x)(5x)
with (2)(3)
(x)(3)
and (5x)(2)
3x and 10x will yield 13x
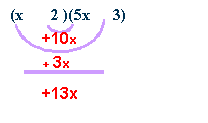
(x
+ 2)(5x + 3) |
|
|
|
|
|
|
 |
|
|
|
|
|
|
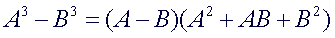
![]()
![]()
![]()
![]()


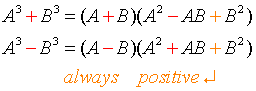
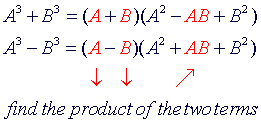
![]()
![]()
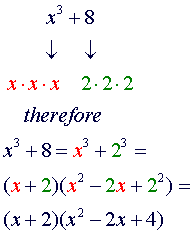
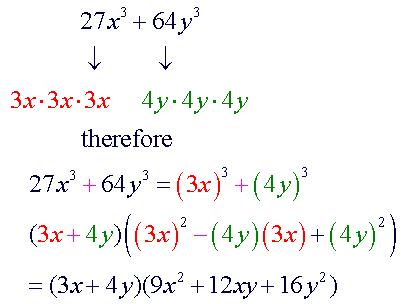
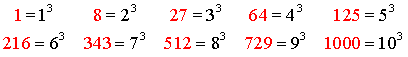
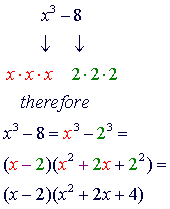
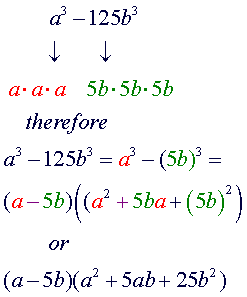
![]()