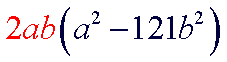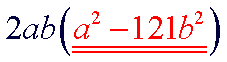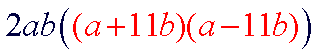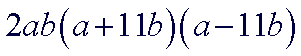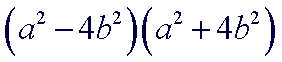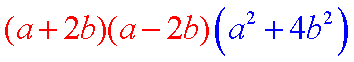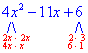EXAMPLE 1

Factor: 

     
  This expression  has two terms. There is a common factor of 2ab. Begin by factoring out the common factor.

 
The remaining factor is a binomial that is the difference of two squares. This factor must be factored using the difference of two squares technique.

Each of the new factors must in turn be checked for further factoring. In this case, no further factoring can be done. Our final answer is 2ab(a+11b)(a-11b)

Return         Example 2       Example 3

 

 

 

 

 

EXAMPLE 2

Factor: 

     
    This expression  has two terms with no common factor. If it is factorable, it must be by binomial techniques. In this case we have the difference of two squares.  

 

Notice that each factor is a binomial. Further factoring may be required. The first factor is the difference of squares and therefore factorable. Factor this factor. The second factor is prime.

HINT:
Variables whose exponents are even will always be perfect squares:  

 

etc.

 
No further factoring can be done. Each of the binomials is prime. The final answer, therefore is (a+2b)(a-2b)(a2+4b2)

NOTE: 
Once the binomial factors contain first degree terms, no further factoring will be possible using the binomial techniques. 

Return         Example 1       Example 3

 

 

 

 

 

 

 

 

 

 

EXAMPLE3 

 

Factor: 

     

 
  This expression  has three terms. There is common factor shared by ALL three terms. Factor out the GCF first.

 

The remaining trinomial may be factored further. 
          

   (4x)(2) +(x)(3)=8x+3x=11x
Therefore:

 

 

NOTE:
Since the leading term is negative, we will make the GCF negative. When factoring out a negative GCF, all the signs of the polynomial change.

 
   

 

 

  

Return         Example 1       Example 2