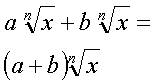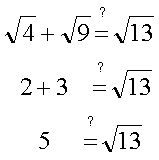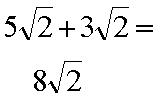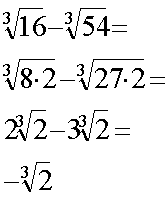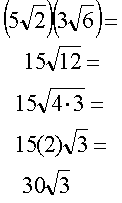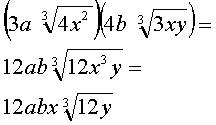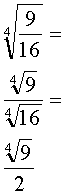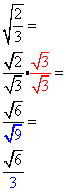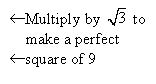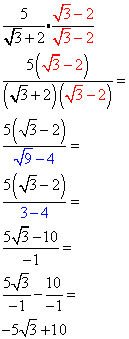Operations with Radicals

 

 

Simplification     Addition and Subtraction     Multiplication     Division

 

 

 

 

 

 

 

 

Simplification of Radicals Rule Example

Use the two laws of radicals to

  1. express the radicand as a product of perfect powers of n and "left -overs"

  2. separate and simplify the perfect powers of n.

SHORTCUT:
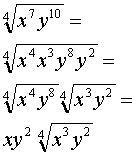
Divide the index into each exponent of the radicand. The whole number part of the quotient will be the exponent on the simplified factor while the remainder will be the exponent on the factor remaining in the radical.

 

 
Top

Simplification     Addition and Subtraction     Multiplication     Division

 Radiacals Main Menu
 

 

 

 
Addition and Subtraction of radicals Rule Example

Simplify all radicals.

Combine only like radical terms:
 same radicand
same index

Combine like radicals by combining the coefficients of the radical terms. The coefficient is the factor that sits outside the radical to the left.

Note:

           
cannot be combined. Here is an example to convince you:

Example 1:

 

  Example 2:   

 
Top

Simplification     Addition and Subtraction     Multiplication     Division

Radiacals Main Menu
 

 

 

 
Multiplication of radicals Rule Example

If the indices are the same

  • Multiply the coefficients

  • Multiply the radicands

  • Simplify the radical.

NOTE: You may simplify the radicals before multiplying. However, you may need to simplify the radical again once you have found the product.

 

Example 1:

 

Example 2: 

Top

Simplification     Addition and Subtraction     Multiplication     Division

 Radiacals Main Menu
 

 

 

 
Division Rule Example
NOTE:  A simplified radical contains no fractions and no radicals in the denominator.

Division Type I: 
Simplify the radical

 

 

                        

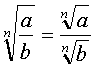
Division Type II:
Rationalize the denominator

  1.  If the denominator is a one-termed radical expression, multiply the numerator and the denominator by a radical that will make the radicand of the denominator a perfect-n.

 

  

 

  1. If the denominator is a binomial in which one or both terms contain a square root, multiply numerator and denominator by the conjugate.

 (a + b) and (a - b) are conjugates:  middle signs are opposite. 

Multiplying by conjugates gives the difference of squares:

(a + b)(a - b) = a2 - b2

 

  1. Multiply numerator and denominator by the conjugate of the denominator.

  2. Multiply the binomials in the denominator.

  3. Simplify the denominator. Note: all radicals should be eliminated.

  4. Continue to simplify the fraction as much as possible.
Top

Simplification     Addition and Subtraction     Multiplication     Division

 Radiacals Main Menu